Distributions - Patch Clamp Handbook

Distributions are a fundamental part of understand your data. The way you data is distributed will determine the way you analyze it and are the fundamental component of most statistical test. In the previous chapter we talked about different data types. You should have a good understanding of what data types are before starting this chapter. This chapter will cover the distributions associated with the continuous and count data types that we covered in the previous chapter.

In the previous chapter we covered terminology associated with describing your data and basic ways to visualize your data. Two ways that we covered, histograms and KDEs, help visualize the distribution of your data (technically a non-parametric distribution). However, these are non-parametric distributions and most statistical tests require parametric distributions so we need to find the distribution that best matches our data. We can discribe distributions as probability density functions (PDF) for continuous variables or probability mass functions (PMF) for discrete/count variables.

There are two fundamental properties of distributions.

Distributions integrate (i.e. the area under the curve) to 1 when you take the distribution from negative limit to positive limit (which can be -infinity to infinity).
Distributions return a likelihood if they are a PDF and a probability if they are a PMF. Likelihood is not the same as a probability. Because the probability of getting any one continuous number is 0 we return a likelihood instead.

You will also often see cumulative distribution functions (CDFs). The CDF is the just the integral of the PDF and the PDF the derivative of the CDF. When taking the integral of a continous function you can just use a Numpy cumsum and multiply by your delta X to get the CDF if you have evenly spaced samples. For the area under the curve you can use a variety of functions provided by scipy such as the trapezoid, simpson, or the romberg. Below we will plot the PDF and CDF for each of the distributions.

For this tutorial, there are interactive samples. Not all of these examples use the preferred way of working with distributions in Python. The recommended way is to use the Scipy stats module. The stats module distributions provide a lot of useful features but can be a little bit intimidating to start with. Scipy stats distributions can provide PDF/PMFs, CDFs, PPFs and fit distributions to your data using maxmimum likelihood.

If you want to learn a little more about PDFs and PMFs I suggest watching Very Normal on Youtube.

import math
import warnings
from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from bokeh.io import output_notebook, show
from bokeh.layouts import column, row
from bokeh.models import ColumnDataSource, CustomJS, Select, Slider, Whisker
from bokeh.plotting import figure
from scipy import stats

warnings.filterwarnings("ignore", category=RuntimeWarning)

cwd = Path.cwd().parent / "data/pv"
df = pd.read_csv(cwd / "mini_data.csv")

output_notebook()

Gaussian distribution¶

In terms of data that we collect in electrophysiology the gaussian distribution is actually not that common but most of the time the visualization methods and statistical tests we use assume our data follows a gaussian distribution. Some non-gaussian distributions, such as the beta and von Mises (radians) distributions, can coverge to a normal distribution with certain parameters. The are problems when you assume that non-gaussian data follows a gaussian distribution AND you do not check your statistical models. We will cover that in the statistics chapter. The gaussian distribution has two parameters, the mean and standard deviation. The mean is what is called a location parameter and shifts the distribution around. The standard deviation is related to the spread of data symetrically around the mean. Technically the gaussian distribution is unbounded. This means that you can get any value from - $\infty$ to + $\infty$ . However, due to limits that we have on computers we generally don’t show all the values up to +/- $\infty$ , but only up to a couple standard deviations past the mean on each side. The equation for the gaussian PDF is:

\frac{1}{\sqrt{2\pi\sigma^2}}\exp\frac{(x-\mu)^2}{2\sigma^2}

(1)

Below you can see how changing the mean and standard deviation changes the magenta distribution relative to the grey reference distribution. We plot both the PDF and the CDF (the integral of the PDF). There are a couple things to note. The area under the curve of the PDF will always equal 1. Changing the standard deviation decreases the likelihood of getting any value but increases the range of likely values you can get.

mu = 0
std = 1
x = np.linspace(mu - std * 4, mu + 4 * std, num=400)
y = np.exp(-((x - mu) ** 2) / (2 * std**2)) / np.sqrt(2 * np.pi * std**2)
source = ColumnDataSource(
    {
        "x": x,
        "y": y,
        "yc": np.cumsum(y) * 0.020050125313283207,
    }
)
pdf = figure(height=250, width=350, title="PDF")
pline = pdf.line("x", "y", source=source, color="magenta")
pline1 = pdf.line(x, y, color="grey")
cdf = figure(height=250, width=350, title="CDF")
cline = cdf.line("x", "yc", source=source, color="magenta")
cline1 = cdf.line(source.data["x"], source.data["yc"], color="grey")

mu = Slider(start=-10, end=10, value=0, step=0.5, title="Mu (mean)")
std = Slider(start=0.1, end=10, value=1, step=0.5, title="Sigma (std)")
callback = CustomJS(
    args={
        "source": source,
        "mu": mu,
        "std": std,
    },
    code="""
    const arr = [];
    const start = mu.value-std.value*4
    const end = mu.value+std.value*4
    const step = (end - start) / (400 - 1);

    for (let i = 0; i < 400; i++) {
        arr.push(start + step * i);
    }
    const temp_y = arr.map(x => {
        const coefficient = 1 / Math.sqrt(2 * Math.PI * Math.pow(std.value, 2));
        const exponent = -Math.pow((x - mu.value), 2) / (2 * Math.pow(std.value, 2));
        return coefficient * Math.exp(exponent);
    })
    const cumsum = [temp_y[0]]
    for (let i = 1; i < 400; i++) {
        cumsum.push((cumsum[i-1] + temp_y[i]));
    }
    source.data.y = temp_y;
    source.data.x = arr;
    source.change.emit();
""",
)

mu.js_on_change("value", callback)
std.js_on_change("value", callback)
show(column(row(mu, std), row(pdf, cdf)))

Lognormal distribution¶

The lognormal distribution is a distribution where if you log transform the data you will get the normal distribution. If your data has a right skew (long tail to the right) your data may follow a lognormal distribution. You may ask why not just log transform the data? Log transforming means your data will no longer be in the same scale which makes downstream interpretations more complicated. The lognormal distribution is very common in biological sciences. Things like rates, lengths, concentrations and energies often follow a lognormal distribution. The lognormal distribution bounds are (0,+ $\infty$ ), The () brackets are exclusive which means that you can never have a 0 in the distribution since any log of 0 is undefined. The PDF of the lognormal distribution is:

\frac{1}{x\sigma\sqrt{2\pi\sigma^2}}\exp(\frac{-(ln(x)-\mu)^2}{2\sigma^2})

(2)

mu = 0
std = 1
x = np.linspace(0.000001, np.exp(mu) + 4 * np.exp(std), num=400)
y = np.exp(-((np.log(x) - mu) ** 2) / (2 * std**2)) / (
    x * std * np.sqrt(2 * np.pi * std**2)
)
source = ColumnDataSource(
    {
        "x": x,
        "y": y,
        "yc": np.cumsum(y) * 0.020050125313283207,
    }
)
pdf = figure(height=250, width=350, title="PDF")
pline = pdf.line("x", "y", source=source, color="magenta")
pline1 = pdf.line(x, y, color="grey")
cdf = figure(height=250, width=350, title="CDF")
cline = cdf.line("x", "yc", source=source, color="magenta")
cline1 = cdf.line(source.data["x"], source.data["yc"], color="grey")

mu = Slider(start=0, end=10, value=0, step=0.5, title="Mu (mean)")
std = Slider(start=0.25, end=10, value=1, step=0.25, title="Sigma (std)")
callback = CustomJS(
    args=dict(
        source=source,
        mu=mu,
        std=std,
    ),
    code="""
    const arr = [];
    const start = 0.00001;
    const end = Math.exp(mu.value)+Math.exp(std.value)*4;
    const step = (end - start) / (400 - 1);

    for (let i = 0; i < 400; i++) {
        arr.push(start + step * i);
    }
    const temp_y = arr.map(x => {
        const coefficient = 1 / (Math.sqrt(2 * Math.PI * Math.pow(std.value, 2))*x*std.value);
        const exponent = -Math.pow((Math.log(x) - mu.value), 2) / (2 * Math.pow(std.value, 2));
        return coefficient * Math.exp(exponent);
    })
    const cumsum = [temp_y[0]]
    for (let i = 1; i < 400; i++) {
        cumsum.push((cumsum[i-1] + temp_y[i]));
    }
    source.data.y = temp_y;
    source.data.x = arr;
    source.data.yx = cumsum;
    source.change.emit();
""",
)

mu.js_on_change("value", callback)
std.js_on_change("value", callback)
show(column(row(mu, std), row(pdf, cdf)))

Gamma distribution¶

The gamma distribution is another important distribution for neuroscience data. The gamma distribution is used to model waiting times and rates. A lot of data we collect are rates, such as mini or spike frequency. If your data has a right skew (long tail to the right) your data may follow a gamma distribution. Interestingly, gamma distributed variables often maximize the information content of a signal which is useful in the brain. The gamma distribution is the generalization the exponential, Erlang and chi-squared distribution. The gamma distribution is defined by a shape, $\alpha$ , and scale, $\theta$ , parameter. Similar to the lognormal distribution the gamma distribution bounds are (0,+ $\infty$ ). The PDF of the gamma distribution is:

\frac{1}{\Gamma(\alpha)\theta^{\alpha}}x^{\alpha-1}e^{-x/\theta}

(3)

$\Gamma$ is the Gamma function is the factorial function that is generalized to complex numbers (except non-positive complex numbers)

You can also get the mean: $\mu=\alpha\theta$ and variance: $\sigma^{2}=\alpha\theta^2$ of the distribution.

shapes = [1.0, 1.25, 1.25, 2.0, 3.0, 5.0, 7.5]
scales = [2.0, 2.0, 3.0, 2.0, 2.0, 1.0, 1.0]
x = np.linspace(0, 20, num=400)
keys = []
glines = {}
cdflines = {}
gamma_fig = figure(height=250, width=350)
gamma_cdf = figure(height=250, width=350)

for i, j in zip(shapes, scales):
    pdf = stats.gamma.pdf(x, i, scale=j)
    cdf = stats.gamma.cdf(x, i, scale=j)
    k = f"a={i} theta={j}"
    keys.append(k)
    glines[k] = gamma_fig.line(x, pdf, color="grey")
    cdflines[k] = gamma_cdf.line(x, cdf, color="grey")
select = Select(title="Option:", value="a=1.0 theta=2.0", options=keys)
glines["a=1.0 theta=2.0"].glyph.line_color = "magenta"
glines["a=1.0 theta=2.0"].glyph.line_width = 3
cdflines["a=1.0 theta=2.0"].glyph.line_color = "magenta"
cdflines["a=1.0 theta=2.0"].glyph.line_width = 3
callback = CustomJS(
    args=dict(
        glines=glines,
        cdflines=cdflines,
        select=select,
    ),
    code="""
    for (let key in glines) {
        if (select.value == key) {
            glines[key].glyph.line_color = 'magenta';
            cdflines[key].glyph.line_color = 'magenta';
            glines[key].glyph.line_width = 3;
            cdflines[key].glyph.line_width = 3;
        }
        else {
            glines[key].glyph.line_color = 'grey';
            cdflines[key].glyph.line_color = 'grey';
            glines[key].glyph.line_width = 1;
            cdflines[key].glyph.line_width = 1;
        }
    }
""",
)

select.js_on_change("value", callback)
show(column(select, row(gamma_fig, gamma_cdf)))

Beta distribution¶

The beta distribution is used to model data that has finite intervals, and proportions and percentages. Some bounds values you might see in neuroscience are correlations (-1,1) and PPR (if you use the percentage formula and not the ratio). The beta distribution’s bound are (0,1) so if you have bounded data that is not between those you can transform it. The beta distribution is defined by a shape, $\alpha$ , and scale, $\beta$ , parameter. The PDF of the beta distribution is:

\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta ) (\alpha ,\beta )}}

(4)

$\Gamma$ is the Gamma function is the factorial function that is generalized to complex numbers (except non-positive complex numbers). The denominator of the PDF is a normalization factor to ensure the distribution has a total probability of 1.

One thing that you will notice is that the beta distribution can take on a wide range of shapes. This makes is very powerful for oddly shaped distributions. It can even even model normally distribution and uniformally distribution data when $\alpha$ = $\beta$

You can also get the mean: $\mu=\frac{\alpha}{\alpha+\beta}$ and variance: $\sigma^{2}=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$ of the distribution.

shapes = [0.5, 5, 1, 2, 5, 1.25, 1, 5]
scales = [0.5, 1, 3, 2, 2, 5, 1, 5]
x = np.linspace(0, 1, num=400)
keys = []
blines = {}
cdflines = {}
beta_fig = figure(height=250, width=350)
beta_cdf = figure(height=250, width=350)

for i, j in zip(shapes, scales):
    pdf = stats.beta.pdf(x, i, j)
    cdf = stats.beta.cdf(x, i, j)
    k = f"a={i} b={j}"
    keys.append(k)
    blines[k] = beta_fig.line(x, pdf, color="grey")
    cdflines[k] = beta_cdf.line(x, cdf, color="grey")
select = Select(title="Option:", value="a=0.5 b=0.5", options=keys)
blines["a=0.5 b=0.5"].glyph.line_color = "magenta"
blines["a=0.5 b=0.5"].glyph.line_width = 3
cdflines["a=0.5 b=0.5"].glyph.line_color = "magenta"
cdflines["a=0.5 b=0.5"].glyph.line_width = 3
callback = CustomJS(
    args=dict(
        blines=blines,
        cdflines=cdflines,
        select=select,
    ),
    code="""
    for (let key in blines) {
        if (select.value == key) {
            blines[key].glyph.line_color = 'magenta';
            cdflines[key].glyph.line_color = 'magenta';
            blines[key].glyph.line_width = 3;
            cdflines[key].glyph.line_width = 3;
        }
        else {
            blines[key].glyph.line_color = 'grey';
            cdflines[key].glyph.line_color = 'grey';
            blines[key].glyph.line_width = 1;
            cdflines[key].glyph.line_width = 1;
        }
    }
""",
)

select.js_on_change("value", callback)
show(column(select, row(beta_fig, beta_cdf)))

Poisson distribution¶

The Poisson distribution is a discete distribution used model the probability of a certain number of events occuring within a time frame thus it models the rate of events. The Poisson distribution assumes that each event is independent of each other. The Poisson distribution is similar to the gamma distribution kind of like the discrete cousin of the gamma distribution. The Poisson distribution has an important related feature called dispersion (technically other distributions also have this but is is particularly useful for the Poisson distribution) or the fano factor: $\frac{\sigma^2}{\mu} = 1$ , which is also related to the coefficient of variation: $\frac{\sigma}{\mu} = \lambda^{-\frac{1}{2}}$ . The fano factor is often used to check the variability of a spike train, minis and any set of data that has events. The closer the fano factor is to 0, then the more predicable the process is, think of a cell spiking everytime at the trough of a 4 Hz sine wave. The farther you go above 1 the more clustered your events will be suggesting that there is some reason your events cluster (make sense for neurons that can fire spike trains). The Poisson PMF is defined by $\lambda, or the rate, and k, the integer value. The Poisson PMF (not PDF since it is distrete) is:$ ${\frac {\lambda ^{k}e^{-\lambda }}{k!}}$ $ On the x-axis you have the number of events that could occur for each number of events that could occur you have probability on the y-axis. Since the Poisson distribution is a discrete distribution you actually get probabilities out instead of likelihoods. One thing to note is that the plot uses scatter instead of a line. This is to indicate that the Poisson distribution can only take integer values.

lam = 1
k = np.arange(0, 21)
y = (lam**k * np.exp(-lam)) / np.array([math.factorial(i) for i in k])
source = ColumnDataSource({"k": k, "y": y, "yc": np.cumsum(y)})
pdf = figure(height=250, width=350, title="PDF")
pline = pdf.scatter("k", "y", source=source, color="magenta")
pline1 = pdf.scatter(k, y, color="grey")
cdf = figure(height=250, width=350, title="CDF")
cline = cdf.scatter("k", "yc", source=source, color="magenta")
cline1 = cdf.scatter(source.data["k"], source.data["yc"], color="grey")

lam = Slider(start=0.5, end=10, value=1, step=0.25, title="Lambda")
callback = CustomJS(
    args=dict(
        source=source,
        lam=lam,
    ),
    code="""
    const arr = [];
    for (let i = 0; i < 21; i++) {
        let result = 1;
        for (let k = 2; k <= i; k++) {
            result *= k;
        }
        const val = ((lam.value**i)*(Math.exp(-1*lam.value)))/result;
        arr.push(val);
    }
    const cumsum = [arr[0]]
    for (let i = 1; i < 21; i++) {
        cumsum.push((cumsum[i-1] + arr[i]));
    }
    source.data.y = arr;
    source.data.yc = cumsum
    source.change.emit();
""",
)

lam.js_on_change("value", callback)
show(column(row(lam), row(pdf, cdf)))

Fitting your data to a distribution¶

In this next section we will look at how data fits to different distributions. Due to limitations of the format we will stick with IEI data however, I encourage to you modify the code below on either the other data we have or better yet on your own data. You should note that it is quite hard to accurately describe your data with distributions as you will see. Part of this is the limitation of the tools we have to fit a distribution to our data and that our data are messy due to measurement noise, recording conditions, etc. We will fit a gamma and lognormal distribution to the IEI data with and without a transform.

You will also notice that the gamma distribution does not fit very well with the untransformed data. You will also notice how the normal, lognormal and gamma distribution converge as the transform gets stronger. The biggest problem with IEI data is that it is tightly clusters around the mode and has a long tail to the right (right-skew). The mode can be estimated by looking at peak of the KDE. Many models assume some relationship between the mean and the variance of the data so the functions have limited types of shapes that they can support. For all the models that we used, the lognormal distribution is the best. This is probably because it is parameterized the same way as the normal distribution. Another thing to think about is that earlier we showed how we can model IEIs by randomly distributing events over time. Why does our data here not match that data? When we put TTX in the bath minis (mE/IPSCs, not sE/IPSCs) should be randomly distributed over time. One reason is that we cannot resolve mini events that are overlapping. This leads to a lognormal like distribution where we can occasionally resolve overlapping events and small amplitude events. Additionally, there are mini events that are smaller than the noise of the recording so we will miss those minis but it does not mean they do not exist. We have two factors which are simply limitations of the technique we are using which could change the distribution of the data that we collect.

Lastly, when Scipy fits data to a distribution it will modify the location of the distribution which usually does not occur when fitting regression models if the model does not explicitly contain a location parameter (of which the normal distribution is one of the few that explicity contain it). So if you want to run a regression model (t-test, ANOVAs included) you may need to shift your data to just above 0 to improve the fit if you are using a gamma, beta or lognormal distribution. Additionally, Scipy fits distributions using Maximum Likelihood Estimation. There are other methods such as Expectation Maximization and Bayesian statistics that can fit distributions.

dist_data = df.loc[df["IEI (ms)"] > 0, "IEI (ms)"]


def fit_distributions(data):
    dist_dict = {}

    min_val = min(data)
    max_val = max(data)
    padding = (max_val - min_val) * 0.1  # Add 10% padding
    grid_min = min_val - padding
    grid_max = max_val + padding
    grid_min = max(grid_min, 0)
    positions = np.linspace(grid_min, grid_max, num=248)
    kernel = stats.gaussian_kde(data)
    y = kernel(positions)
    dist_dict["kde_x"] = positions
    dist_dict["kde_y"] = y

    # Gaussian distribution fit
    norm_vals = stats.norm.fit(data)
    dist_dict["norm_x"] = np.linspace(1e-10, data.max() + 1e-10, 248)
    dist_dict["norm_y"] = stats.norm.pdf(
        dist_dict["norm_x"], loc=norm_vals[0], scale=norm_vals[1]
    )

    # Lognormal distribution fit
    logvals = stats.lognorm.fit(data)
    dist_dict["lognorm_x"] = np.linspace(1e-10, data.max() + 1e-10, 248)
    dist_dict["lognorm_y"] = stats.lognorm.pdf(
        dist_dict["lognorm_x"], logvals[0], loc=logvals[1], scale=logvals[2]
    )

    # Gamma distribution fit
    gammavals = stats.gamma.fit(data)
    dist_dict["gamma_x"] = np.linspace(1e-10, data.max() + 1e-10, 248)
    dist_dict["gamma_y"] = stats.gamma.pdf(
        dist_dict["lognorm_x"], gammavals[0], gammavals[1], gammavals[2]
    )

    return dist_dict


def create_fig(source, title):
    fig = figure(height=250, width=400, title=title)
    fig.line("lognorm_x", "lognorm_y", source=source, line_color="magenta")
    fig.line("norm_x", "norm_y", source=source, line_color="orange")
    fig.line("gamma_x", "gamma_y", source=source, line_color="blue")
    fig.line("kde_x", "kde_y", source=source, line_color="black", line_width=3)
    return fig


source = ColumnDataSource(fit_distributions(dist_data))
fig = create_fig(source, title="No transform")

sqrt_source = ColumnDataSource(fit_distributions(np.sqrt(dist_data)))
sqrt_fig = create_fig(sqrt_source, title="Sqrt")

log10_source = ColumnDataSource(fit_distributions(np.log10(dist_data)))
log10_fig = create_fig(log10_source, title="Log10")

legend = figure(y_range=(5, 5), height=250, width=400, title="Legend")
legend.line(
    [0, 1], [0, 0], line_color="magenta", line_width=3, legend_label="lognormal"
)
legend.line([0, 1], [1, 1], line_color="orange", line_width=3, legend_label="normal")
legend.line([0, 1], [3, 3], line_color="blue", line_width=3, legend_label="gamma")
legend.line([0, 1], [4, 4], line_color="black", line_width=3, legend_label="kde")
legend.legend.location = "center"

show(column(row(fig, sqrt_fig), row(log10_fig, legend)))

Based on the data you will see that the best fit for this IEI data is probably a lognormal distribution. If you want to run stats on the IEI data you will probably need to transform the data or use a lognormal distribution. This is true even though the IEIs should be exponentially distribution. Lastly, the lognormal distribution is interesting because it is everywhere. If you want to read more about the different neural processes that lognormally distributed you can read more in The log-dynamic brain: how skewed distributions affect network operations Buzsáki & Mizuseki, 2014.

Describing a distribution¶

There several ways we can describe distributions: skew, kurtosis, location, and scale. We can also describe distributions in relation to each other such there the distributions exhibit the same variance, homoscedasticity, or differing variance heteroscedasticity. All of these features are important when analyzing your data.

Skew¶

Skew is how asymmetric the data is. We have seen some asymmetric distributions with the gamma and lognormal distribution. Skew also shifts the relationship between the mode, median and mean. Once your data skewed the most points will lie under the mode rather than the mean. The more skewed your data is, the more the mean starts to become affected by the extreme, outlier or influencer values. You can see below examples of different skew and how they affect the mean, median and mode.

fig, ax = plt.subplots(ncols=3, figsize=(10, 3), constrained_layout=True)
ax[0].set_title("Left skew")
i = np.exp(-1)
x = np.linspace(stats.lognorm.ppf(0.001, i), stats.lognorm.ppf(0.999, i), num=200)
y = stats.lognorm.pdf(x, i)
points = stats.lognorm.rvs(i, size=100)
_ = ax[0].plot(x, y, color="black")
_ = ax[0].axvline(x[y.argmax()], c="magenta")
_ = ax[0].axvline(np.median(points), c="blue")
_ = ax[0].axvline(np.mean(points), c="orange")
ax[2].set_title("Right skew")
_ = ax[2].plot(-x, y, color="black")
_ = ax[2].axvline(-x[y.argmax()], c="magenta")
_ = ax[2].axvline(-np.median(points), c="blue")
_ = ax[2].axvline(-np.mean(points), c="orange")
i = 0
x = np.linspace(stats.norm.ppf(0.001, i), stats.norm.ppf(0.999, i), num=200)
y = stats.norm.pdf(x, i)
points = stats.norm.rvs(i, size=100)
ax[1].set_title("No skew")
_ = ax[1].plot(x, y, color="black")
_ = ax[1].axvline(x[y.argmax()], c="magenta")
_ = ax[1].axvline(np.median(points), c="blue")
_ = ax[1].axvline(np.mean(points), c="orange")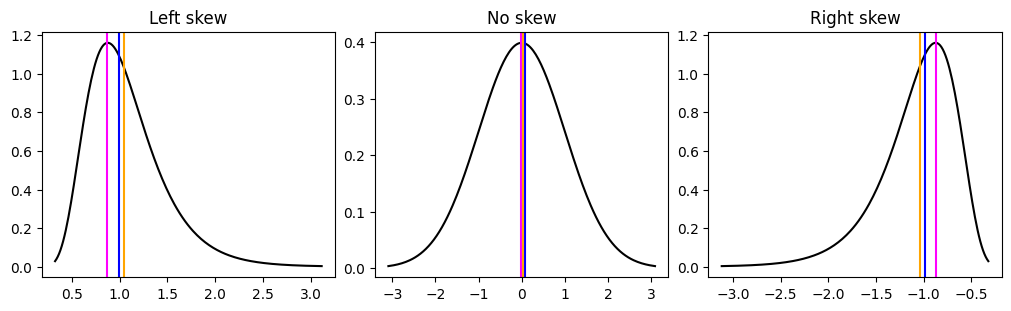

Kurtosis¶

Kurtosis is the tailedness of the data, or how large the tails. While kurtosis is often seen with something called peakedness it is technically separate. The higher the kurtosis the more outliers you will get in your data. Kurtosis is often seen with changes in skew but is separate from skew.

fig, ax = plt.subplots(ncols=3, figsize=(10, 3))
ax[0].set_title("Negative kurtosis (platykurtosis)")
x = np.linspace(stats.uniform.ppf(0.001), stats.uniform.ppf(0.999), num=200)
y = stats.uniform.pdf(x)
_ = ax[0].plot(x, y)
x = np.linspace(stats.norm.ppf(0.001), stats.norm.ppf(0.999), num=200)
y = stats.norm.pdf(x)
ax[1].set_title("No kurtosis")
_ = ax[1].plot(x, y)
x = np.linspace(stats.laplace.ppf(0.001), stats.laplace.ppf(0.999), num=200)
y = stats.laplace.pdf(x)
_ = ax[2].plot(x, y)
_ = ax[2].set_title("Positive kurtosis (leptokurtosis)")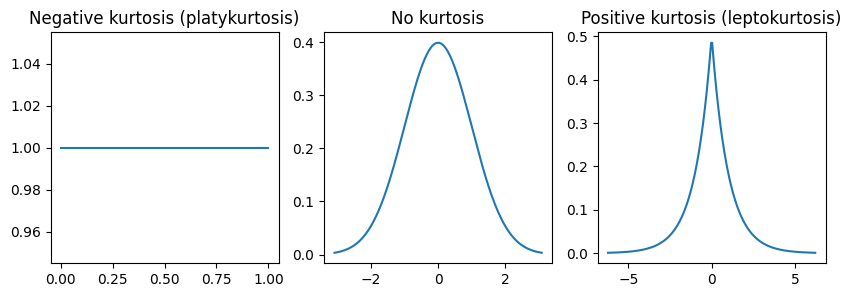

Heteroskedasticity¶

Heteroskedasticity means you have unequal variance (i.e. standard deviation) across groups (like genotype) or as x values increase or decrease. Heteroskedasticity violates one of the key assumptions of regression models, which is homogeniety of variances. Most basic tests such t-test and ANOVAs all assume homogeniety of variances since they use pooled estimates of variance and assume residuals come for a normal distribution with mean 0 and a fixed standard deviation. There are versions of t-test (Welch’s) and ANOVAs/linear regression (robust errors, weighted least squares) can control for heteroskedasticity which we will cover in the statistics chapter.

fig, ax = plt.subplots(ncols=3, figsize=(8, 3), constrained_layout=True)
rng = np.random.default_rng(42)
x = np.linspace(0, 20, num=500)
y = 1.2 * x + 3
rng.normal()
y1 = y + rng.normal(size=500, scale=5)
ax[0].plot(x, y1, ".", alpha=0.6, markeredgecolor="none")
ax[0].set_title("Homoskedastic")
temp = rng.normal(size=500, scale=5) * np.linspace(1, 0.1, num=500)
y2 = y + temp
ax[1].plot(x, y2, ".", alpha=0.6, markeredgecolor="none")
ax[1].set_title("Heteroskedastic")
y1 = rng.normal(size=25, scale=5)
x1 = rng.uniform(0, 1, size=25) * 0.6
y2 = rng.normal(size=25, scale=2)
x2 = rng.uniform(0, 1, size=25) * 0.6 + 1
ax[2].errorbar(
    np.mean(x1), np.mean(y1), xerr=0.3, yerr=np.std(y1), color="black", linewidth=2
)
ax[2].plot(x1, y1, ".", alpha=0.8)
ax[2].errorbar(
    np.mean(x2), np.mean(y2), xerr=0.3, yerr=np.std(y2), color="black", linewidth=2
)
ax[2].plot(x2, y2, ".", color="orange", alpha=0.8)
_ = ax[2].set_title("Heteroskedastic")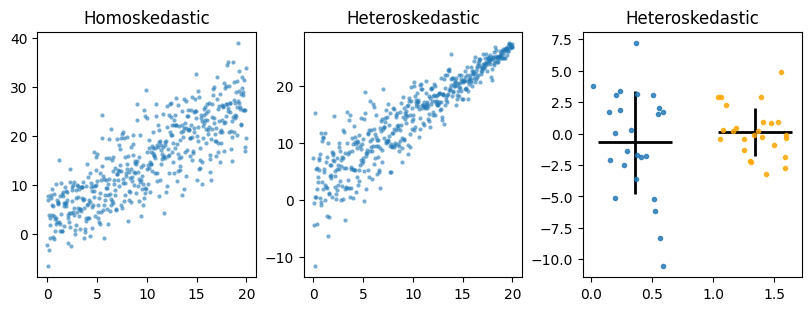

Hopefully at this point you have a better idea of what distributions are and how they represent our data.

References¶

Buzsáki, G., & Mizuseki, K. (2014). The log-dynamic brain: how skewed distributions affect network operations. Nature Reviews Neuroscience, 15(4), 264–278. 10.1038/nrn3687