Miniature/spontaneous postsynaptic currents: Part 1

There are several steps to processing acquisitions to find PSCS (in this case mEPSCs).

Filter the acquisition
Convolution/deconvolution to find events
Clean events

First we are going to import some python packages.

import json
import urllib
from collections import defaultdict

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from bokeh.io import output_notebook, show
from bokeh.layouts import column, row
from bokeh.models import ColumnDataSource, CustomJS, Select, Slider, Spinner
from bokeh.plotting import figure
from scipy import fft, optimize, signal, stats

output_notebook()

Next we are going to load the data. All the data is stored on json files. While this file type is not the most practical for storing electrophysiological data, it is the very convenient since it does not require any third party python packages and can be loaded from a remote source.

temp_path = (
    "https://cdn.jsdelivr.net/gh/LarsHenrikNelson/PatchClampHandbook/data/mepsc/"
)
exp_dict = {}
for index in range(1, 6):
    with urllib.request.urlopen(temp_path + f"{index}.json") as url:
        temp = json.load(url)
        temp["array"] = np.array(temp["array"])[:100000]
        exp_dict[index] = temp
x_array = np.arange(len(exp_dict[1]["array"])) / 10

The first thing to do is look through your data just to see what it looks like. For reference the data in this tutorial is from a layer 5 cell in the ACC of a P16 mouse.

The recorded data is usually in pA, as is the case for this data.
It can be hard to see the events, however this is a parvalbumin interneuron and has very large mEPSC events.
The acquisition mean hovers around -40 pA. This is the amount of current injected to keep the cell at the holding voltage which in this case is -70 mV.

# Initial data
source = ColumnDataSource(
    data={"x": np.arange(100000) / 10, "y": exp_dict[1]["array"][:100000]}
)

# Create a plot
plot = figure(x_axis_label="Time (ms)", y_axis_label="Current (pA)", height=350, width=450)
plot.line("x", "y", source=source, line_color="black")
spinner = Spinner(title="Acquisition", low=1, high=5, step=1, value=1, width=80)

# JavaScript callback to fetch JSON data and update plot
callback = CustomJS(
    args=dict(source=source, spinner=spinner),
    code="""
    let val = spinner.value
    let URL = `https://cdn.jsdelivr.net/gh/LarsHenrikNelson/PatchClampHandbook/data/mepsc/${val}.json`
    fetch(URL)
    .then(response => response.json())
    .then(data => {
        console.log(data)
        source.data.y = data["array"].slice(0,100000);
        source.change.emit();
    })
    .catch(error => console.error('Error fetching data:', error));
""",
)

# Add a button to trigger the callback
spinner.js_on_change("value", callback)

# Layout and show
layout = column(spinner, plot)
show(layout)

First, we will define some important features of the acquisition so that we can reuse the settings throughout the analysis. It is important to note that the all the parameters are going to be in samples. The current files were recorded at 10000 Hz so we multiply the time we want, in milliseconds, time by 10 or divide sample number by 10 to get to milliseconds.

baseline_start = 0
baseline_end = 3000
sample_rate = 10000

Filter the acquisition¶

First thing we need to do is filter the acquisition. There are two ways to filter. You can remove the baseline then lowpass filter or you can apply a bandpass filter. Filtering achieves two goals. The first is remove the DC offset. The DC offset is actually the current need to clamp the voltage. The second goal is to remove extraneous high frequency noise which can hinder the analysis. You can also use notch filter to remove 60 Hz, however I recommend finding ways to reduce 60 Hz before you even record. Notch filters can introduce artifacts into and distort your signal.

For this tutorial we will use remove the baseline by taking the mean and use a zero-phase Butterworth filter with an order 4 filter and a lowpass cutoff of 600 Hz and compare that to a bandpass cutoff of [0.01, 600] to remove the DC offset and high frequency noise. If you want to learn more about filtering checkout the chapter on filtering. For the PSC tutorial we are going to skip the RC check.

Filter method 1: Remove the baseline and lowpass filter¶

for value in exp_dict.values():
    baseline = np.mean(value["array"])
    temp = value["array"] - baseline
    value["holding_current"] = baseline
    sos = signal.butter(4, Wn=600, btype="lowpass", output="sos", fs=sample_rate)
    filt_array = signal.sosfiltfilt(sos, temp)
    value["lowpass"] = filt_array

Filter method 2: Bandpass filter¶

for value in exp_dict.values():
    baseline = np.mean(value["array"])
    temp = value["array"] - baseline
    sos = signal.butter(
        4, Wn=[0.01, 600], btype="bandpass", output="sos", fs=sample_rate
    )
    filt_array = signal.sosfiltfilt(sos, temp)
    value["bandpass"] = filt_array

Let’s compare the two types of filtering. Some things to notice.

Both methods filter almost identically and substantially reduce the noise.
Both methods reduce the size of the mEPSC.
With a zero-phase filter we can prevent any phase changes so the timing of the baseline and peak of the mEPSC events is unchanged.

y = exp_dict[1]["array"] - exp_dict[1]["holding_current"]
fig, ax = plt.subplots(nrows=2)
for i in ax:
    i.axis("off")
_ = ax[0].set_title("Bandpass match")
_ = ax[0].plot(y, c="black", linewidth=1)
_ = ax[0].plot(exp_dict[1]["bandpass"], c="red", linewidth=1)
_ = ax[1].set_title("Lowpass")
_ = ax[1].plot(y, c="black", linewidth=1)
_ = ax[1].plot(exp_dict[1]["lowpass"], c="red", linewidth=1)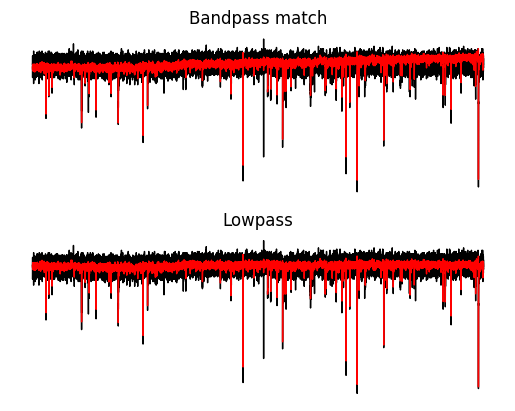

Template matching vs deconvolution¶

There are main two ways, template matching (correlation) and deconvolution, to identify m/sPSCs, both need a template PSC. Convolution is the “traditional” way however I have seen quite a few new papers using a deconvolution method since it is less dependent on the exact template shape. The deconvolution technique was first proposed by Pernia-Andrade Pernía-Andrade et al., 2012. We will cover both methods to see how each works. If you want to learn more about convolution and deconvolution check out the signal processing chapter.

Create a template¶

First we are going to create a template PSC. We will use the same template for each method. The template is a double exponential with a exponential rise multiplied by an exponential decay. You can see the template equation below.

def create_template(
    amplitude: int | float = -20,
    rise_tau: int | float = 0.3,
    decay_tau: int | float = 5,
    risepower: int | float = 0.5,
    length: int | float = 30,
    spacer: int | float = 1.5,
    sample_rate: int = 10000,
) -> np.ndarray:
    """Creates a template based on several factors.

    Args:
        amplitude (float): Amplitude of template
        rise_tau (float): Rise tau (ms) of template
        decay_tau (float): Decay tau (ms) of template
        risepower (float): Risepower of template
        length (float): Length of time (ms) for template
        spacer (int, optional): Delay (ms) until template starts. Defaults to 1.5.

    Returns:
        np.array: Numpy array of the template.
    """
    if rise_tau == decay_tau:
        rise_tau += 0.001
    s_r_c = sample_rate / 1000
    rise_tau = int(rise_tau * s_r_c)
    decay_tau = int(decay_tau * s_r_c)
    length = int(length * s_r_c)
    spacer = int(spacer * s_r_c)
    template = np.zeros(length + spacer)
    t_length = np.arange(0, length)
    offset = len(template) - length
    Aprime = (decay_tau / rise_tau) ** (rise_tau / (rise_tau - decay_tau))
    y = (
        amplitude
        / Aprime
        * (
            (1 - np.exp(-t_length / rise_tau)) ** risepower
            * np.exp((-t_length / decay_tau))
        )
    )
    template[offset:] = y
    return template

You can use the interactive plot below to see how the different parameters effect the template mEPSC. There is more on curves in the curves chapter.

template = create_template(decay_tau=2.5)
source = ColumnDataSource({"x": np.arange(template.size) / 10, "y": template})

plot = figure(width=400, height=400)

plot.line(np.arange(template.size)/10, template, color="black")
plot.line("x", "y", source=source, line_width=3, line_alpha=0.6, line_color="magenta")

rise_tau = Slider(start=0.5, end=10, value=0.5, step=0.5, title="Rise tau (ms)")
risepower = Slider(start=0.5, end=10, value=0.5, step=0.25, title="Rise power")
decay_tau = Slider(start=0.75, end=50, value=3, step=0.25, title="Decay tau (ms)")
amplitude = Slider(start=-60, end=-5, value=-20, step=0.5, title="Amplitude (pA)")
length = Slider(start=20, end=70, value=30, step=1, title="Length (ms)")

callback = CustomJS(
    args=dict(
        source=source,
        rise_tau=rise_tau,
        decay_tau=decay_tau,
        amplitude=amplitude,
        length=length,
        risepower=risepower,
    ),
    code="""
    if (rise_tau === decay_tau) {
        rise_tau += 0.001;
    }
    const s_r_c = 10
    const rt = Math.round(rise_tau.value * s_r_c)
    const dt = Math.round(decay_tau.value * s_r_c)
    const len = Math.round(length.value * s_r_c)
    const spacer = 15
    const y = new Array(len+spacer).fill(0)
    const t_length = Array.from({ length: len }, (_, i) => 0 + i)
    const Aprime = (dt / rt) ** (rt / (rt - dt))
    const temp_y = t_length.map(x => {
        return amplitude.value / Aprime * ((1 - Math.exp(-x / rt)) ** risepower.value * Math.exp(-x / dt))
    })
    y.splice(spacer, temp_y.length, ...temp_y);
    const x = Array.from({ length: len+spacer }, (_, i) => 0 + i/10)
    source.data = { x, y }
    source.change.emit();
""",
)

rise_tau.js_on_change("value", callback)
decay_tau.js_on_change("value", callback)
amplitude.js_on_change("value", callback)
length.js_on_change("value", callback)

show(row(plot, column(rise_tau, decay_tau, amplitude, length)))

Create a template¶

For the analysis of mEPSCs on parvalbumin interneurons we just need to modify the decay rate of the template since PV cell mEPSCs tend to have a very fast decay compared to other cell types (think about why this might be related to the function of PV cells in the larger circuit).

template = create_template(decay_tau=2.5)

Method 1: Template matching¶

Template matching essentially slides the template along the acquisition and correlates the template with the segment of the acquisition it is currently aligned with. I do some extract work to ensure the template matched array is zero phase relative to the original array. This makes it easier to find PSC events.

for value in exp_dict.values():
    temp_match = np.correlate(value["lowpass"], template, mode="full")
    temp_match = temp_match[template.size - 1 :]
    value["temp_match"] = temp_match

Method 2: Deconvolution¶

Deconvolution essetially divides out the template from the acquisition. Deconvolution is inherently noisy so the deconvolve output has to be filtered to even see the signal.

for value in exp_dict.values():
    kernel = np.hstack((template, np.zeros(len(value["lowpass"]) - len(template))))
    template_fft = fft.fft(kernel)
    signal_fft = fft.fft(value["lowpass"])
    temp = signal_fft / template_fft
    temp = np.real(fft.ifft(temp))
    sos = signal.butter(4, Wn=300, btype="lowpass", output="sos", fs=sample_rate)
    deconvolved = signal.sosfiltfilt(sos, temp)
    value["deconvolved"] = deconvolved

Now let’s compare the two methods.You will notice that peaks end up in approximately the same place and are positive. These peaks are where putative mEPSCs are occuring. There are two major differences. One is that the deconvolved array has a stable baseline which can make event finding easier. The second is that peaks in the deconvolved array are narrower but shorter.

index = 1
fig, ax = plt.subplots(nrows=2)
for i in ax:
    i.axis("off")
_ = ax[0].set_title("Template match")
_ = ax[0].plot(exp_dict[1]["temp_match"], c="black", linewidth=1)
_ = ax[1].set_title("Deconvolved")
_ = ax[1].plot(exp_dict[1]["deconvolved"], c="black", linewidth=1)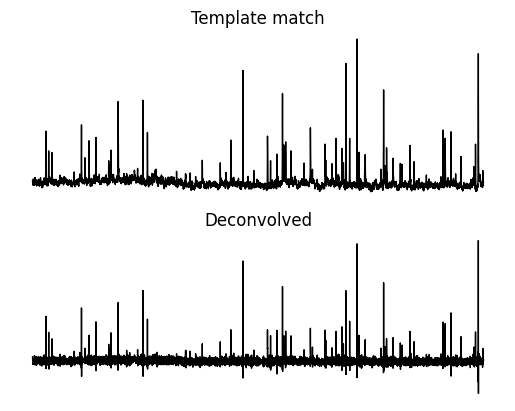

Finding events¶

The next step involves finding peaks where . For each method we will need to define some threshold so that we don’t pick up on the small peaks that are noise. For finding events we will use a way I devised that helps create a per acquisition normalization which allows using a single threshold value for difference acquisitions. First we will get the RMS without the peaks. We will use that to adjust a single threshold value. Finally we will use Scipy find_peaks to find the events above the threshold.

def get_percentile_rms(deconvolved_array: np.ndarray) -> float | float:
    # Get the top and bottom 2.5% cutoff.
    bottom, top = np.percentile(deconvolved_array, [2.5, 97.5])

    # Return the middle values.
    middle = np.hstack(
        deconvolved_array[
            np.argwhere((deconvolved_array > bottom) & (deconvolved_array < top))
        ]
    )
    # Calculate the mean and rms.
    mu = np.mean(middle)
    rms = np.sqrt(np.mean(np.square(middle - mu)))

    return mu, rms

Template matching¶

sensitivity = 3.5
mini_spacing = 100

for value in exp_dict.values():
    mu, rms = get_percentile_rms(value["temp_match"])
    peaks, _ = signal.find_peaks(
        value["temp_match"] - mu,
        height=sensitivity * (rms),
        distance=mini_spacing,
        prominence=rms,
    )
    value["temp_match_events"] = peaks

Deconvolution¶

sensitivity = 4
mini_spacing = 100

for value in exp_dict.values():
    mu, rms = get_percentile_rms(value["deconvolved"])
    peaks, _ = signal.find_peaks(
        value["deconvolved"] - mu,
        height=sensitivity * (rms),
        distance=mini_spacing,
        prominence=rms,
    )
    value["deconvolved_events"] = peaks

temp_match_x = exp_dict[index]["temp_match_events"]
deconvolved_x = exp_dict[index]["deconvolved_events"]
fig, ax = plt.subplots(nrows=2)
_ = ax[0].set_title("Template match")
_ = ax[0].plot(exp_dict[1]["temp_match"], c="black", linewidth=1)
_ = ax[0].plot(temp_match_x, exp_dict[1]["temp_match"][temp_match_x], ".", c="orange")
_ = ax[1].set_title("Deconvolved")
_ = ax[1].plot(exp_dict[1]["deconvolved"], c="black", linewidth=1)
_ = ax[1].plot(deconvolved_x, exp_dict[1]["deconvolved"][deconvolved_x], ".", c="magenta", linewidth=1)
for i in ax:
    i.axis("off")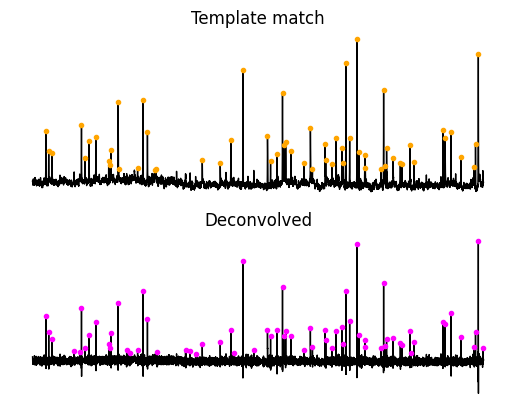

Let’s see where these events are in the original acquisition. Most of the time you will see that purple and orange dots are falling just before the event. You will notice that many of the events found from both methods are in the same place but the smaller event locations seem to be most different between the two methods. You will notice that some locations do not seem to have an event and that is okay because these will be screened out at the next step.

array = exp_dict[index]["lowpass"]
temp_match_x = exp_dict[index]["temp_match_events"]
deconvolved_x = exp_dict[index]["deconvolved_events"]
fig, ax = plt.subplots(nrows=2)
_ = ax[0].set_title("Template match")
_ = ax[0].plot(array, c="black", linewidth=1)
_ = ax[0].plot(temp_match_x, array[temp_match_x], ".", c="orange")
_ = ax[1].set_title("Deconvolved")
_ = ax[1].plot(array, c="black", linewidth=1)
_ = ax[1].plot(temp_match_x, array[temp_match_x], ".", c="magenta", linewidth=1)
for i in ax:
    i.axis("off")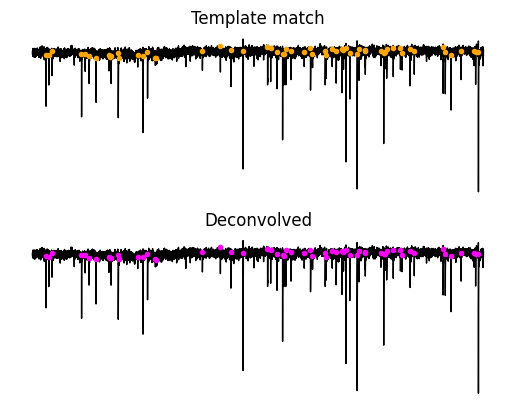

Analyzing events¶

The analysis from this point on will get much harder. The are many parameters for many events that we will need to assess and keep track of. There are several ways that you can optimally store and retrieve data in Python. We will primarily use Python dictionaries which are general container, however if you want to create a program your self I would recommend using classes. Since this tutorial is focused on analyzing the data rather than developing an optimal program we will stick with the basics.

One important factor to note is that for any method analyzing events noise is always an issue. The quality of the events and the parameters we retrieve will depend on how noisy the acquisitions are. Noise acquisitions make it hard to find the baseline and peak of events. Noise makes it hard to determine what is a real event and what a bad event. For this reason good mini analysis programs tend to let you add and remove events as well as change the baseline and peak of events. There are many do not have interactive features. This tutorial is limited in that it will be very hard to modify event parameters that are incorrect since we do not have a fully interative UI. However, I think that it is extremely useful to see and think about how events are found.

For the next step we are going to analyze the events we have found. We will go through the following steps:

Create the event start and stop
Find the event peak.
Find the baseline. You need the baseline to calculate the amplitude and after finding the baseline.
Find the event decay with a simple estimate.
Find the event decay with curve fitting.
Clean the events.

After finding these parameters we calculate other parameters such as rise time, rise rate and amplitude of the event. Since it is computationally fast to compute these other values, it is beneficial to save on memory and just compute them as needed.

Finding the event start and stop¶

The method of finding events that we have used usually places the event marker just before the start of the event. We will create a window around the event. We will need to define how long we want an event. For mEPSCs 30 ms is usually long enough. We will also need to define how much earlier the event should start compared to the event position. For now 2 ms is good enough. Because we are working in samples we will have to convert both of the times to samples. Since our sample rate is 10000 Hz we need to multiply each time by 10 which we will use many times so we will save it as a variable s_r_c (sample rate correction).

def create_event(
    event_array: np.ndarray, event_position: int, event_length: int, offset: int
):
    array_start = int(event_position - offset)
    end = int(event_position + event_length)
    if end > len(event_array) - 1:
        array_end = len(event_array) - 1
    else:
        array_end = end
    array_start = max(0, array_start)
    array_end = min(array_end, array.size)
    return array_start, array_end


s_r_c = 10
offset = 2 * s_r_c
event_length = 30 * s_r_c
for value in exp_dict.values():
    value["events"] = []
    array = value["array"]
    for p in value["deconvolved_events"]:
        event = {}
        start, stop = create_event(array, p, event_length, offset)
        event["start"] = start
        event["stop"] = stop
        event["event_position"] = p
        value["events"].append(event)

Finding the peak¶

There are a couple ways to find the peaks of the event. If your event placement is good enough you can just use min or max depending on the direction of currents/voltages. However, this fails if your event window contains another event which is not that uncommon or if you have noise in your recording. I use an interative method to find the peak. First we use a prominence based peak finding method. If any peaks are found then we will check that we peak we found is not just noise. If that fails then we use a order based peak finding where a peak is just a value that is larger than all the values within 4 ms on both sides. You could simply find the minimum/maximum value, however I found that in practice this does not work very well.

def peak_corr(event_array, peak: int, s_r_c):
    peaks_2 = signal.argrelextrema(
        event_array[:peak],
        comparator=np.less,
        order=int(0.4 * s_r_c),
    )[0]
    peaks_2 = peaks_2[peaks_2 > peak - 4 * s_r_c]
    if len(peaks_2) == 0:
        event_peak_x = peak
    else:
        peaks_3 = peaks_2[event_array[peaks_2] < 0.85 * event_array[peak]]
        if len(peaks_3) == 0:
            event_peak_x = peak
        else:
            event_peak_x = peaks_3[0]
    event_peak_y = event_array[int(event_peak_x)]
    return event_peak_x, event_peak_y


def find_peak_alt(event_array, offset):
    peaks = signal.argrelextrema(event_array, comparator=np.less, order=int(3 * s_r_c))[
        0
    ]
    peaks = peaks[peaks > offset]
    if len(peaks) == 0:
        event_peak_x = np.nan
        event_peak_y = np.nan
    else:
        event_peak_x, event_peak_y = peak_corr(event_array, peaks[0], s_r_c)
    return event_peak_x, event_peak_y


def find_peak(event_array, offset, s_r_c):
    peaks, _ = signal.find_peaks(
        -1 * event_array,
        prominence=4,
        width=0.4 * s_r_c,
        distance=int(3 * s_r_c),
    )
    peaks = peaks[peaks > offset]
    if len(peaks) == 0:
        event_peak_x, event_peak_y = find_peak_alt(event_array, offset)
    else:
        event_peak_x, event_peak_y = peak_corr(event_array, peaks[0], s_r_c)
    return event_peak_x, event_peak_y


for value in exp_dict.values():
    for p in value["events"]:
        event_array = value["lowpass"][p["start"] : p["stop"]]
        offset = p["start"] - p["event_position"]
        peak_x, peak_y = find_peak(event_array, offset, 10)
        peak_x += p["start"]
        p["peak_x"] = peak_x

Finding the baseline¶

There are two ways to find the baseline. One is to use a slope and find when the slope stops increasing. This method needs several additions to make it work well. The other way is to assume that the baseline of your event is around 0 mV. The problem with this method is that if your acquisition meanders around 0 mV you can find very weird baselines. We will use the slope method with modifications I have found work very well.

def find_baseline(event_array, event_peak_x, event_peak_y, s_r_c):
    baselined_array = event_array - np.max(event_array[:event_peak_x])
    peak = int(event_peak_x)
    search_start = np.argwhere(baselined_array[:peak] > 0.35 * event_peak_y).flatten()
    if search_start.size > 0:
        slope = (event_array[search_start[-1]] - event_peak_y) / (
            peak - search_start[-1]
        )
        new_slope = slope + 1
        i = search_start[-1]
        while new_slope > slope and i > 0:
            slope = (event_array[i] - event_peak_y) / (peak - i)
            i -= 1
            new_slope = (event_array[i] - event_peak_y) / (peak - i)
        baseline_start = signal.argrelmax(
            baselined_array[int(i - 1 * s_r_c) : i + 2], order=2
        )[0]
        if baseline_start.size > 0:
            baseline_x = int(baseline_start[-1] + (i - 1 * s_r_c))
            if baseline_x < 0:
                baseline_x = 0
        else:
            baseline_x = int(baseline_start.size / 2 + (i - 1 * s_r_c))
            if baseline_x < 0:
                baseline_x = 0
    return baseline_x


for value in exp_dict.values():
    array = value["lowpass"]
    for p in value["events"]:
        event_array = array[p["start"] : p["stop"]]
        baseline_x = find_baseline(
            event_array, p["peak_x"] - p["start"], array[p["peak_x"]], 10
        )
        p["baseline_x"] = baseline_x + p["start"]

Estimating the decay¶

Next we will estimate the decay of the events. You can estimate the decay by finding the time when the signal is 1/3 the amplitude. One thing to note is that we have just been keeping track of the x sample where each point of interest occurs. However, with the estimate decay we will interpolate y so we will collect the y value as well since interpolating requires a bit more work.

def est_decay(event_array, baseline, peak_x):
    peak_y = event_array[peak_x]
    baselined_event = event_array - baseline
    x_array = np.arange(event_array.size)
    return_to_baseline = int(
        (np.argmax(baselined_event[peak_x:] >= (peak_y - baseline) * 0.25)) + (peak_x)
    )
    decay_y = event_array[peak_x:return_to_baseline]
    if decay_y.size > 0:
        est_tau_y = ((peak_y - baseline) * (1 / np.exp(1))) + baseline
        decay_x = x_array[peak_x:return_to_baseline]
        event_tau_x = np.interp(est_tau_y, decay_y, decay_x)
    else:
        event_tau_x = np.nan
        est_tau_y = np.nan
    return event_tau_x, est_tau_y


for value in exp_dict.values():
    array = value["lowpass"]
    for p in value["events"]:
        event_array = array[p["start"] : p["stop"]]
        baseline = array[p["baseline_x"]]
        tau_x, tau_y = est_decay(event_array, baseline, p["peak_x"] - p["start"])
        p["tau_x"] = tau_x + p["start"]
        p["tau_y"] = tau_y

Curve fitting the decay¶

We will curve fit the decay for a more accurate measure of the decay. We will use a double exponential decay. If you want to try fitting a single exponential decay I challenge you to look at the code below and figure it out. One thing we will do is run the decay fit using a try except statement since the fit can fail and it is hard to predict when it will fail. You will also notice that we are using what is called a double exponential decay. This is simply two exponentials added together. You could fit a single or even triple exponential decay. Doulbe exponential decay tends to give a pretty good fit. Since the exponential decays are additive you just add the fast and slow decay tau together to get your decay fit. If you want to know more about curve fitting check out the the curves chapter.

def exp_decay_offset(x, amplitude, tau, amp_offset):
    y = (amplitude * np.exp((-x) / tau)) + amp_offset
    return y


def fit_decay(event_array, est_tau, s_r_c):
    try:
        x_array = np.arange(event_array.size) / s_r_c
        upper_bounds = [0.0, np.inf, np.inf]
        lower_bounds = [-np.inf, 0.0, -np.inf]
        init_param = np.array([event_array[0], est_tau, 0.0])
        popt, _ = optimize.curve_fit(
            exp_decay_offset,
            x_array,
            event_array,
            p0=init_param,
            bounds=[lower_bounds, upper_bounds],
        )
        amplitude, tau, amp_offset = popt
        output = {
            "amplitude": amplitude,
            "tau": tau,
            "amp_offset": amp_offset,
        }
    except (RuntimeError, ValueError):
        output = {
            "amplitude": np.nan,
            "tau": np.nan,
            "amp_offset": np.nan,
        }
    return output


for value in exp_dict.values():
    array = value["lowpass"]
    for p in value["events"]:
        est_tau = p["tau_x"] - p["peak_x"]
        temp = int(est_tau * 1.5) + p["peak_x"]
        stop = min(temp, p["stop"])
        event_array = array[p["peak_x"] : p["stop"]]
        decay_fit = fit_decay(event_array, est_tau / 10, 10)
        p["decay_fit"] = decay_fit

Lets look at all the analysis to see how well it worked. There is a least one instance where two events occured close together and only one event was analyzed. The are a couple events where the place of a baseline or peak may not be optimal.

index = 1
y = exp_dict[index]["lowpass"]
events = exp_dict[index]["events"]
mfig = figure(height=300, width=600, output_backend="webgl")
x = np.arange(array.size)
mfig.line(x, y, color="black")
for i in events:
    start = i["start"]
    stop = i["stop"]
    mfig.line(x[start:stop], y[start:stop], color="magenta")

    # Plot curve fit
    if not np.isnan(i["decay_fit"]["amplitude"]):
        start = i["peak_x"]
        fit_x = np.arange(stop - start) / 10
        fit_y = exp_decay_offset(fit_x, **i["decay_fit"])
        mfig.line(x[start:stop], fit_y, color="#06DBE2")

# Plot baseline
peak_x = [i["baseline_x"] for i in exp_dict[index]["events"]]
peak_y = [y[i] for i in peak_x]
mfig.scatter(peak_x, peak_y, color="grey", marker="plus", size=7)

# Plot peaks
peak_x = [i["peak_x"] for i in exp_dict[index]["events"]]
peak_y = [y[i] for i in peak_x]
mfig.scatter(peak_x, peak_y, color="orange", size=7)

# Plot tau
tau_x = [i["tau_x"] for i in exp_dict[index]["events"] if not np.isnan(i["tau_x"])]
tau_y = [i["tau_y"] for i in exp_dict[index]["events"] if not np.isnan(i["tau_y"])]
mfig.scatter(tau_x, tau_y, color="#06DBE2", marker="triangle", size=7)

show(mfig)

Rise time¶

Rise time can be calculated using the slope of the linear of the rise that occurs at the 10-90% portion between the baseline and peak of the synaptic current or you can calculate is an easier way by just measuring the time between the baseline and peak. Both are technically correct but you might see the 10-90% method more often. The 10-90% method can be useful if you are not sure of the exact location of the baseline and peak or if you have noise recordings. You can also use 20-80% if your confidence in the location of the baseline start and peak is more uncertain. Measuring from the baseline to peak is probably more controversial but I feel confident enough in how my algorithm to find the baseline and peak work that I go with the more simple method. Additionally the 10-90% method will not work on very small currents even if they are good. The rise occurs very quickly and you may be left with very few points to get an accurate measure unless you up the sample rate of your recordings.

Rise rate¶

The rise rate is the just the slope the linear fit of the rise between the 10-90% or just the amplitude divided by the rise time.

Next we are going to calculate all the other parameters, amplitude, rise time and rise rate.

for value in exp_dict.values():
    array = value["lowpass"]
    for p in value["events"]:
        p["rise_time"] = (p["peak_x"] - p["baseline_x"]) / 10
        p["amplitude"] = np.abs(array[p["peak_x"]] - array[p["baseline_x"]])
        p["rise_rate"] = p["amplitude"] / p["rise_time"]
        p["est_tau"] = (p["tau_x"] - p["peak_x"]) / 10

Finally we will exclude events based on amplitude, rise time, decay time. Some of the settings may be a little bit redundant however, I have found this to be pretty robust in excluding events. It is common to exclude events that:

Have a rise time that is too fast (usually 0.5ms is a good starting point)
Have a rise time that is too slow. This will depend on the type of m/sEPSC you are analyzing. Inhibitory events have a slow rise time compared to excitatory events.
Amplitude that is too small. The minimum amplitude is depends on your signal to noise. I have found that PV interneurons have a particularly high signal noise ratio (good) where as MSNs have a much lower signal to noise ratio so the amplitude setting is 4 pA vs 6 pA respectively.
Decay time that is too short. This really helps remove events that are just noise since noise tends to be symmetrical.
Decay faster than rise. This is a boolean. Usually if the decay tau is faster than the rise the event is just noise.

def check_event(event, event_criteria, prior_peaks, prior_peak=0, fs=10000) -> bool:
    """The function is used to screen out events based
    on several values set by the experimenter.

    Args:
        event (MiniEvent): An analyzed MiniEvent
        events (list): List of previous events

    Returns:
        Bool: Boolean value can be used to determine if
        the event qualifies for inclusion in final events.
    """
    # Retrieve the peak to compare to values set
    # by the experimenter.
    s_r_c = fs / 1000
    event_peak = event["peak_x"]

    # The function checks, in order of importance, the
    # qualities of the event.
    if np.isnan(event_peak) or event_peak in prior_peaks:
        return False
    elif (
        (event_peak - prior_peak) / s_r_c < event_criteria["mini_spacing"]
        or event["amplitude"] <= event_criteria["amp_threshold"]
        or event["rise_time"] <= event_criteria["min_rise_time"]
        or event["rise_time"] >= event_criteria["max_rise_time"]
        or event["est_tau"] <= event_criteria["min_decay_time"]
        or event["start"] > event_peak
    ):
        return False
    elif event_criteria["decay_rise"] and (event["est_tau"] <= event["rise_time"]):
        return False
    else:
        return True


event_criteria = {
    "decay_rise": False,
    "max_rise_time": 10,
    "min_rise_time": 0.1,
    "amp_threshold": 4,
    "mini_spacing": 2,
    "min_decay_time": 0.5,
}
for value in exp_dict.values():
    prior_peak = 0
    accepted_events = []
    event_peaks = set()
    for event in value["events"]:
        check = check_event(event, event_criteria, event_peaks, prior_peak)
        if check:
            accepted_events.append(event)
            prior_peak = event["peak_x"]
    value["accepted_events"] = accepted_events

Final data inspection¶

Finally we have cleaned our data. It is time to pull all the data and see how it looks.

Gather the data¶

gathered_data = []
events = []
time_add = 0
for key, value in exp_dict.items():
    output = defaultdict(list)
    array = value["lowpass"]
    for event in value["accepted_events"]:
        output["Peak (ms)"].append(event["peak_x"] / 10)
        output["Timestamp (ms)"].append(event["peak_x"] / 10 + time_add)
        output["Est Tau (ms)"].append(event["est_tau"])
        output["Rise Time (ms)"].append(event["rise_time"])
        output["Rise Rate (pA/ms)"].append(event["rise_rate"])
        output["Amplitude (pA)"].append(event["amplitude"])
        output["Fit Amplitude (pA)"].append(event["decay_fit"]["amplitude"])
        output["Fit Tau (ms)"].append(event["decay_fit"]["tau"])
        output["Amp Offset (pA)"].append(event["decay_fit"]["amp_offset"])
        start = event["start"]
        stop = event["stop"]
        events.append(array[start:stop])
        output["Start (ms)"].append(start)
    output["IEI (ms)"] = [
        output["Peak (ms)"][i] - output["Peak (ms)"][i - 1]
        for i in range(1, len(output["Peak (ms)"]))
    ]
    output["IEI (ms)"].extend([0] * int(
        len(output["Peak (ms)"]) - len(output["IEI (ms)"])
    ))
    output["Acquisition"].extend([key] * len(output["Peak (ms)"]))

    output["Holding Current (pA)"].extend([value["holding_current"]]*len(output["Peak (ms)"]))

    time_add += 10000

    gathered_data.append(output)

final_data = defaultdict(list)
for item in gathered_data:
    for key, value in item.items():
        final_data[key].extend(value)

max_event_length = max([len(i) for i in events])
events_array = np.zeros((len(events), max_event_length))
index = 0
for e in events:
    events_array[index, : len(e)] = e
    index += 1

Inspect the data¶

At this point we just want to see how if our data changes over time and as a distribution. The reason we want to see our data over time is if there are any tight clusters of points or increases or decreases. This could indicate that something changed with your recording. You could have deleted an aquisition, added a drug to the bath, the tissue could have moved, your carbogen could have run out, access resistance could change, your cell could be dying, etc. The reason we want to look a distribution is to see how the data is distributed. Most the PSC features do not have a normal distribution. Additionally we want to see if there is any biomodality to our data. You should get a distribution with a single mode even though the data is not normally distribution.

figure1 = figure(height=250, width=400)
figure2 = figure(height=250, width=400)

columns = [
    "Est Tau (ms)",
    "Rise Time (ms)",
    "Amplitude (pA)",
    "Rise Rate (pA/ms)",
    "Fit Amplitude (pA)",
    "Fit Tau (ms)",
    "IEI (ms)",
]
variable_dict = {key: final_data[key] for key in columns}
variable_dict["IEI (ms)"] = final_data["IEI (ms)"] + [0] * int(
    len(final_data["Est Tau (ms)"]) - len(final_data["IEI (ms)"])
)
for key, value in variable_dict.items():
    variable_dict[key] = [[0, i] for i in value]

source1 = ColumnDataSource(variable_dict)

hist_dict = {}
for i in columns:
    data = final_data[i]
    if i == "IEI (ms)":
        data = np.array(data)
        data = data[data > 1e-6]
    if i == "Fit Tau (ms)":
        data = np.array(data)
        data = data[data < 100]
    if i == "Fit Amplitude (pA)":
        data = np.array(data)
        data = np.abs(data[data > -300])
    min_val = min(data)
    max_val = max(data)
    padding = np.abs(max_val - min_val) * 0.1  # Add 10% padding
    grid_min = min_val - padding
    grid_max = max_val + padding
    grid_min = max(grid_min, 0)
    positions = np.linspace(grid_min, grid_max, num=124)
    kernel = stats.gaussian_kde(data)
    y = kernel(positions)
    hist_dict[f"{i}_x"] = positions
    hist_dict[f"{i}_y"] = y

hist_dict["y"] = hist_dict["Amplitude (pA)_y"]
hist_dict["x"] = hist_dict["Amplitude (pA)_x"]
source2 = ColumnDataSource(hist_dict)


mline = figure1.multi_line(
    [[i, i] for i in final_data["Timestamp (ms)"]],
    source1.data["Amplitude (pA)"],
    line_width=1,
    line_alpha=0.6,
    line_color="black",
)
line = figure2.line(x="x", y="y", source=source2, line_color="black")

menu = Select(
    title="Variables",
    value=columns[0],
    options=columns,
)

callback = CustomJS(
    args=dict(
        source1=source1,
        source2=source2,
        mline=mline,
        line=line,
        menu=menu,
    ),
    code="""
    mline.data_source.data.ys = source1.data[menu.value];
    mline.data_source.change.emit();
    line.data_source.data.y = source2.data[`${menu.value}_y`];
    line.data_source.data.x = source2.data[`${menu.value}_x`];
    line.data_source.change.emit();
""",
)

menu.js_on_change("value", callback)

show(column(row(menu), row(figure1, figure2)))

Final events¶

Finally we will plot all the PSCs together as a scaled and unscaled version. Scaling events (between 0 and 1) is useful for determining whether the events are coming from the same population since different populations of events tend to have different rise and decay times, and different amplitudes.

scaled_events = events_array - events_array.max(axis=1, keepdims=True)
scaled_events /= abs(scaled_events.min(axis=1, keepdims=True))
x = np.arange(events_array.shape[1]) / 10
source1 = ColumnDataSource(
    {"x": [x for _ in np.arange(events_array.shape[0])], "events": list(events_array), "scaled_events": list(scaled_events)}
)
source2 = ColumnDataSource(
    {
        "x": x,
        "avg_event": events_array.mean(axis=0),
        "avg_scaled": scaled_events.mean(axis=0),
    }
)
fig, ax = plt.subplots(ncols=2)
for i in ax:
    i.axis("off")
_ = ax[0].plot(events_array.T, c="black", linewidth=1, alpha=0.2)
_ = ax[0].plot(events_array.mean(axis=0),linewidth=1, c="orange")
_ = ax[0].set_title("Events")
_ = ax[1].plot(scaled_events.T, c="black", linewidth=1, alpha=0.2)
_ = ax[1].plot(scaled_events.mean(axis=0), linewidth=1, c="magenta")
_ = ax[0].set_title("Scaled Events")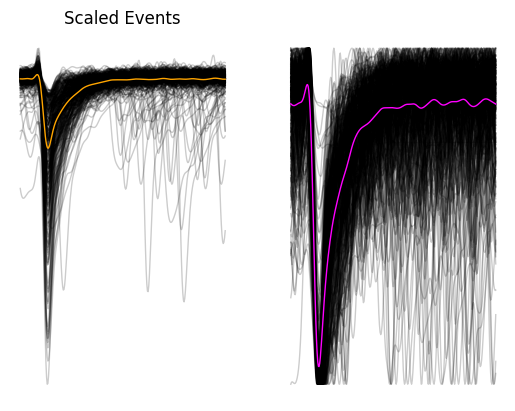

Export the data¶

df = pd.DataFrame(final_data)
df.to_csv("mini_data.csv", index=False)
np.savetxt("mini_events.csv", events_array, delimiter=",")

Check out the next part of the m/sPSC analysis to see how the features we collected compare between cells types.

References¶

Pernía-Andrade, A. J., Goswami, S. P., Stickler, Y., Fröbe, U., Schlögl, A., & Jonas, P. (2012). A Deconvolution-Based Method with High Sensitivity and Temporal Resolution for Detection of Spontaneous Synaptic Currents In Vitro and In Vivo. Biophysical Journal, 103(7), 1429–1439. 10.1016/j.bpj.2012.08.039

Chapters

Miniature/spontaneous postsynaptic currents

Chapters

Miniature/spontaneous postsynaptic currents: Part 2